前回記事では「Haig説、Morris説、および高野説を併せて批判する」という副題を掲げていましたが、Morris説についてはTakano(1998)中の引用との関連で言及した限りで批判したまでで、そこで全体としてのMorris説について批判にはなっていませんでした。ただこれまで読込んだ限りで感じることは、既存の諸説についてOptical explanateion、Explanation based on symmetry、Physical rotation、Mental rotation、などと命名しているのですが、こういう命名が諸説をどこまで的確に表現しているか、あるいはこういう名称がその後に一人歩きして他人の研究に影響を与えすることで混乱が生じていないか、かなり危ういものを感じます。特に「Symmetry(対称性)に基づいた説明」を単に「Symmetry」という単語だけで見出しとして使用していることは非常に問題だと思います。
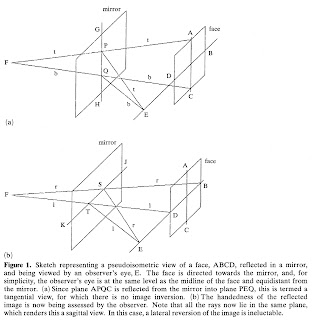
さて、前回記事と前々回記事ではHaig説における2通りの説明のうち最初の説明を私が高く評価していることがご理解いただけると思います。だからこそ、Haig説を「たらいの中の赤ん坊」に喩え、赤ん坊を流してしまったMorris説と高野説を批判していたわけです。というのも、この説明では鏡映反転において比較される対象は何(何と何)かという、本質的でありながら意外と忘れられがちな問題を浮び上がらせているからです。今回もまた同じ図を転載します:
この図では鏡像が表現されていません。それというのもHaig氏は光線という物理的な存在だけで説明しようとしているからですが、同じような状況で鏡像を表現した図を私が作成したことがあり、次にその図を掲げます:
この図ではHaig(1993)の点Eに相当するのが(A)で、Eの共役点Fに相当するのが(A2)です。
さて、鏡像問題のテーマそのものである「Reversal」、「逆転」、「反転」、「変換」などが論じられる際に、鏡像はいったい何に対して逆転しているのかを規定せざるを得ないはずですが、それがどうも自明と言うわけには行きません。初期の論文であるPears(1952)には「Counterpart」と表現されています。確かにそうですが、これでは何のことか分かりません。大抵の著述では「Object」あるいは日本語の場合「実物」と表現されることが多いようです。
「実物」と表現されることは一見、自明のように見えますが、本当に自明といえるでしょうか?自己鏡像の場合は言葉の上から当然、「自分自身」ということになり、多くの著者はそのように表現しています。しかし、肩から下の自分自身で見える部分は別として、自分自身では絶対に直接見ることのできない顔や頭部について、どうして逆転が観察できるのでしょうか?
他者鏡像の場合は確かに鏡像と同様に他者そのものを直接眺めることができ、場合によっては同一視野の中で同時に見比べることもできます。しかし幾何光学が明らかにしているところによれば、鏡像はその他者の表面から発散する光線が鏡に反射することで観察者の眼に見えるのであり、光線を眼で受け止めることによって見ているという点で、鏡を介さずに見る場合と全く同じです。つまり、他者から出る光線がいわば二手に分かれて違う方向から観察者の眼に到達することで2つの像を見ているのであり、その人物自身を見ているという点で両者に違いはありません。したがって、鏡映反転における「逆転」は「鏡像と実物(物体自体、本人自身)」との関係であるとは言えないのです。
以上のように、逆転は鏡像と、いわば直視像との2つの像を比較した上で観察されるものであり、一方が他方に「Transform」あるいは「変換」されたなどと考えることは誤った結論に導かれる原因になりかねません。
鏡像と対になる、あるいは比較される対象が「実物(物自体)」ではなく「直視像」とでも言うべき「像」であるといえる根拠は他にいくつも挙げることができます。例えば:
◆ 鏡像も直視像も照明光の存在で生じるものであるのに対し、物自体は常に存在している
◆ 色や平面パターンは眼で観察することで始めて認知されるものである。つまり物自体ではなく像に生じる属性である
◆ 物の形状は幾何学的な計測で把握し、表現できるとしても、結局のところすべては感覚に基づいているのであり、そのようなデータも結局のところ「像」と言うほかはない
今は思いつかないものの他にも根拠はいくつも挙げられるように思います。
(以下、3月29日の追記です)
最後に、鏡映の関係が何と何との関係であるかを明らかにすることは鏡像問題の根本であり、これを曖昧にしたり取り違えたままでは鏡像問題になりません。高野説は、文字の鏡映反転認知は文字の記憶と比較することで生じるとしています。このプロセスはレオナルド・ダ・ヴィンチが使ったと言われる反転文字、いわゆる鏡文字が通常の文字とは逆転していることに気付くプロセスと何も変わりません。ただ逆転に気付くというだけの話であって、こうなればもう鏡像問題そのものを放棄したに等しいといえます。
(以上、2017年3月27日、29日 田中潤一)
「意味」にまつわる意味深長で多様なテーマを取り上げています。 2011年2月13日から1年間ほどhttp://yakuruma.blog.fc2.com に移転して更新していましたが、2011年12月28日より当サイトで更新を再開しました。上記サイトは現在『矢車SITE』として当ブログを含めた更新情報やつぶやきを写真とともに掲載しています。
2017年3月27日月曜日
2017年3月15日水曜日
鏡像の意味論その15 ― (光学的)虚像について ― Haig説、Morris説、および高野説を併せて批判する
鏡像の「像」、英語ではMirror Imageの「Image」とは何でしょうか?
幸いなことに、語源についてはいざ知らず、日本語の像と英語のimageはだいたい同じ意味で(専門用語としても一般用語としても)使われているようです。 ただ日本語の「像」は漢字の熟語として使われる意外には単独ではあまり使われず、かわりに「イメージ」が使われることが多いですね。
「像」も「イメージ」も実に多様な意味で使われています。そういったわけで像とは何かという議論になるとあまりにも多岐にわたる議論になって、とても収拾がつかなくなるでしょうし、鏡像問題の枠を超えてしまいます。ただし、鏡像問題で重要な要素である光学あるいは幾何光学的に定義される「像」については、明確にして理解しておく必要があります。というのも、そもそも鏡像が光の存在下で生じていることはまあ、光学の知識などを知らなくても普通の人なら理解しているとはいえますが、なぜ実際に鏡で見ているように見えるのかということは、光学の知識なしでは絶対に理解できないからです。本当は眼のしくみについても理解しなければならないはずですが、それは当面ブラックボックスに入れておくとしても、光の直進と反射の理屈を知る必要があります。
鏡映反転の謎はプラトンを悩ませたと言われています。プラトンのような超天才でも鏡映反転の謎が解けなかった理由の少なくとも一つは、プラトンの時代には幾何光学が成立していなかったためでしょう。プラトンは幾何学者ではあったけれども幾何光学はまだ存在もしていなかったというわけですね。しかしプラトンは当時のあり合わせの知識で安易な説明を付けて満足するようなことはしなかったわけで、これは逆にプラトンが真の科学者でもあったことを示すものだと思います。
ということで、鏡映反転の問題がまともに議論されるようになったのは光学の、少なくとも光の直進と反射の法則が明らかになった後、つまりヨーロッパのルネッサンス時代以降のことになるのではないでしょうか。 たとえば哲学者のカント。
数学者で科学者でもあったカントが鏡映反転の問題を考えたと言われています。これは私見ですが、カントはどうも鏡映反転の問題を考えているうちに、いつしかもっと抽象的な空間の問題に移行してしまい、具体的な鏡映反転の問題を置き去りにしてしまったように思います。というのは鏡映反転の問題からもっと抽象的な空間の問題に移行することで、後の学者などによって幾何学的な対掌体の概念がやがて明らかになってくるからです。ここではこういう歴史的な問題は余談ということにしておきます。(注:私はプロレゴ-メナの日本語訳しかカントの著作は知らないので、上記カントの考察について考えたことは、プロレゴ-メナから読み取れる限りのことです。)
さて、以上のような次第で幾何光学の基礎、少なくとも幾何光学における像の定義を知らずに鏡映反転のメカニズムを考察することは現代では無意味であることが分かります。
とは言え、幾何光学で「像」の概念が完璧に定義されているかといえば、必ずしもそうはいえず、「像」の本質を問うような議論はあまりされていないのではないでしょうか? ただし、幾何光学(この場合は結像光学という分野もあるようですが)で取り扱われる限りの実像と虚像の定義、少なくともそれらの像が成立する位置や大きさなどは厳密に定義されているはずで、それらを正しく扱わない限り、幾何光学を論じること自体が無意味です。
日本人の場合、少なくとも高校までに幾何光学の基礎、光の直進と反射の理論については習っているのではないでしょうか?例え習っただけで十分に理解していないとしても、 少なくとも専門家には鏡像成立のメカニズムが理解されていることを納得しているので、鏡を見ても不思議に思わず、安心していられるのではないでしょうか。光の反射による鏡映のメカニズムが知られるまでは、鏡の作用は日本でも神秘現象だったのです。もっとも何らかの自然現象であるらしいことは経験的に分かっていたでしょうし、多分、江戸時代くらいにもなれば、殆どの場合は特別な神秘現象ではないらしいという程度のことも経験的には感づいていたとは思いますが。とは言え、鏡や水面の向こう側にこちら側の景色が映って見えること自体は謎であり、不思議なことだったのです。幾何光学によって少なくとも大幅にこの謎が解明されたわけですから、幾何光学の理論を無視したり、理解せずに鏡映反転の謎を解くことは無謀であり、知的後退と言わざるをえません。
ただ、現在の科学は数多くの専門分野にわかれており、例えば小林秀雄もどこかで、「科学者も自分の専門分野以外のことでは素人と変わらない」と書いていたように記憶しています。 それは全くそのとおりでしょう。前回に考察したHaig氏の説明を見ても、Haig氏は心理学者を、「光学を知らない」ということで批判していますが、当のHaig氏は光という物理的な存在について考察しているだけで、「像」という物理的ではない存在については非常に無理解のままです。一方の高野先生は幾何光学の基本的な概念を理解していません。これについてはHaig氏の心理学者に対する批判がそのまま該当するのかも知れません。
そうはいっても、科学が多くの専門分野に分かれているとはいえ、心理学は感覚や知覚の問題を扱わざるを得ないのであって、生理学を通じて物理化学と不可分とも言えるのではないでしょうか。だからこそ、マッハのような物理学者が心理学の発展に貢献しているのではないのでしょうか? ですから、少なくとも知覚心理学のような分野で、特に視覚に関連する分野で幾何光学を正しく、少なくとも必要な範囲で、理解していないことは致命的な結果をもたらすと言わざるを得ません。
そこで前回の続きですが、ここでもう一度Haig論文の図を次に引用します。
前回は私の考えによるHaig説の批判でした。その際、特に必要はなかったのでHaig説の具体的で詳細な説明はしませんでしたが、今回、高野先生によるHaig説批判を検討するに当たってはそうも行かないので、まず簡単にHaig説の主張そのものを要約しておきます。なお、以下の数節は今回のテーマ「虚像について」とは必ずしも関係なく、また煩雑なので、青色文字にしてあります。適当に飛ばしてお読みください。
Haig説では次の2つの異なる方法(どちらも上図に基づいていますが)で鏡映の左右逆転を説明しています。ただし基本的な原因が光の反射の法則にあるとする点が両者に共通しています(Morris氏や高野先生などはこれを「光学仮説」と呼んでいます。要するに幾何光学に基づく説明のことです):
① 上図で顔(face、右側の四角形)から出る光を鏡(mirror、左側の四角形)で反射させてEの位置で見た像を、Fの位置(conjugate point、共役点)で直接見た像と比較すると、上下(AC)は逆にならないが、左右(BD)は逆になる
② 上図で(a)のように入射光の作る面(APQC)と反射光の作る面(PQE)が重ならない方向(Tangential)の場合は方向が逆転しないのに対して(b)のように、入射光の作る面(STBD)と反射光が作る面(STE)が重なる(同一面)場合には方向が逆転して見える
以上の①と②の二通りの説明をしているわけですが、高野先生はまずMorris(1993)を引用して①を否定しています。その根拠は、Eの位置で鏡像を見ている人がFの位置に歩いて移動して直接(鏡を透過させるか鏡を取り除いて)顔を見た場合を鏡像と比較すると確かに左右だけが逆転するが、歩いて移動せずに上から飛び込むように、つまり逆立ちした状態でFの位置まで移動した場合は左右ではなく上下が逆転するではないか?だからHaig説は間違いである、と言うものです。
端的に言ってこのMorris(1993)による批判は間違っています。確かに観察者が上から飛び込むように、つまり逆立ちした状態でEからFに移動したとすれば左右ではなく上下で逆転しますが、だからといって、普通に歩いてEからFに移動した場合に左右が逆転することまでを否定することにはなりません。何れの場合も上下か左右のどちらかで逆転しています。要するにMorris(1993)の説明はHaig説に条件を付けているだけであって、これでHaig説のすべてを全面的に否定することはできないのです。前回記事で私が説明したように、対象が平面であって「鏡映で左右が逆転するのはなぜか?」という問いかけに対する回答である限り、Haig説(上記①の説明)が間違いであるとは言えないのです。
次にTakano()では上記②の説明を、次のように否定しています。「 If his explanation were correct, an up-down reversal would be observed by the eye located on the elongation of AC in Figure I A because the optical layout becomes essentially identical to that in Figure I B, producing what Haig called a "sagittal view" (pp. 864865).」
これは正当な批判であると考えられます。確かにACの延長線上、例えばCの下方で鏡を見た場合は上下方向をHaig(1993)のいう「Sagittal」面で見ているのにも関わらず上下が逆転して見えることにはなりません。この点でHaig説は誤りです。ただし、この説明が誤りであるからといって①の説明までを否定できるわけではありません。①の説明と②の説明は、両者が光反射の法則に基づいている点で共通していますが、一方が否定されたら他方も否定されるという関係ではありません。①の説明が、例え条件付きであっても有効である以上、「光学仮説」を全面的に否定することはできないのです。
Haig説の問題は、「Sagittal」という用語の用い方にもあるようです。手元にあった2つの理化学事典(岩波理化学事典と研究社理化学和英辞典)で調べてみましたが、光学にはSagittal plane、Sagittal rayなどの専門用語があるものの、「回点対称な結像系」で定義される用語だそうです。つまり凸レンズなどによる実像についてのみ、意味を持つ用語ではないかと思います。鏡像は虚像であるし、文字通り鏡面対称であって回転対称な結像系ではなく、光学用語としての「Sagittal」にはあまり意味がないと考えるのですがどうでしょうか。
前回の記事で私は「Sagittal」を解剖学用語として理解したのですが、確かに光学、具体的には結像光学でこの用語が使われているようです。しかし鏡像の問題では結像光学で使われるこの用語と概念に意味はないことになります。ただし、この用語「Sagittal」を解剖学の用語と意味で解釈すると鏡像問題において重要な意味を与えることができます。(解剖学用語としてのSagittalについては、インターネットで画像検索すればすぐに分かります)。
というのは、解剖学用語としての「Sagittal」は人間の上下・前後・左右に関わる用語であるからです。上記Morris(1993)の批判に見られるように、観察者の姿勢と向きは鏡映反転において重要な意味を持っています。ところがHaig説では観察者を含めてすべて1つの点でしか表現されていないのです。そこにSagittalという解剖学にある用語が入ってきたので、私はその前後をきちんと読まずに、ここに観察者の姿勢と方向の要因が加えられているのかなと考えた次第なのです。しかし光学的な定義ではSagittalにさしたる意味はなさそうです。
もしかすると、Haig説では観察者、つまりEで示される眼を持つ観察者の上下・前後・左右の三つの軸の一つである前後軸が、光学でいうSagittal planeという概念にすり替えられているのではないかと思われるのです。上図には観察者は眼の位置だけで表現されています。しかし、観察者が正立して鏡面に向かっていることは暗黙の中に了解されています。Eの位置にいる観察者がFの位置に移動するとすれば、観察者の前後軸と左右軸は逆転しますが、上下軸は逆転しません。長くなるのでこの問題についてはこれまでとします。
以上はHaig説の問題点あるいは誤りと言えますが、今回のテーマである虚像に関連する問題として高野説には上記引用の後の2つの節で重要な誤りが見つかります。引用すると長くなるので省略しますが、次の節とその次の節では、鏡像を、鏡面上に生じた平面パターンのことであると認識した上で議論が展開されています。現に、Haig(1993)からの引用された上図に高野先生が追加された説明には、「The mirror image, PQ, of the vertical line segment,」と書かれていますが、PQをmirror imageというのは明らかな誤りで、幾何光学の定義に反しています。PQは、鏡像でも鏡像中の線分でもありません。前回の記事で私が述べたように、この図には鏡像は表現されていません。この部分を分析してみようと思いましたが、これらの節では「Optical layout」という定義されない曖昧な表現がキーワードのように使われているので、分析するのは非常に難しいです。ただ、この用語が幾何光学で定義されている虚像(この場合は鏡像)を意味しているように受取ることができます。とすれば、高野先生はここで鏡像の二重定義を行っていることになります。これは高野説のその後の展開の基礎になっていますので、この辺の論理を明確にしておくことは重要だと思います。高野先生は鏡像が平面であるという理由で鏡像が相手の対掌体であることを否定しておられますが、幾何光学で定義される鏡像は平面パターンではなく、鏡の表面に生じるものでもないのです。
まず、この文脈で言えばOptical layoutという表現で何を意味しているのかを具体的に、明確にする必要があります。Layoutの本来の意味からは外れますが、上図のような幾何光学の光路図を指しているのでしょうか?その場合は場合によっては具体的にどの図のどの部分であるかを示す必要もあります。あるいは新たに図を作成する必要があるかも知れません。
ここでは、私は専門家でもないので詳しく説明しませんが、幾何光学では鏡像を含めて虚像について厳密にその位置と大きさ、また方向もきちんと定義されています。それらの定義に反する説明は現在の幾何光学の大系そのものを否定することになり、否定するのであればその根拠を示す必要があります。
とはいえ、幾何光学で厳密に定義される虚像というのは、最初の方でも述べましたが、位置とか大きさとか、要するに技術的な展開が可能な範囲でしか定義されず、像そのものについて何ら明確な定義はおこなわれていないように思います。そもそも簡単に辞書的な「定義」で済ませることは不可能な問題であるのかも知れません。しかしそれこそが心理学者、認知科学者、あるいは認識論学者の仕事であり、使命なのではないでしょうか?
虚像について考えることは像そのものについて考える上で最上の手がかりです。
今回の引用参考文献:
Nigel D Haig, 1993 "Reflections on inversion and reversion" Perception1993, volume 22, pages 863-868
Reg C Morris, 1993 "Mirror image reversal: Is what we see what we
present?" Perception, 1993, volume 22, pages 869-876
Yohtaro Takano, 1998 "Why does a mirror image look left-right reversed?
A hypothesis of multiple processes" Psychonomic Bulletin & Review 1998,5 (1), 37-55
幸いなことに、語源についてはいざ知らず、日本語の像と英語のimageはだいたい同じ意味で(専門用語としても一般用語としても)使われているようです。 ただ日本語の「像」は漢字の熟語として使われる意外には単独ではあまり使われず、かわりに「イメージ」が使われることが多いですね。
「像」も「イメージ」も実に多様な意味で使われています。そういったわけで像とは何かという議論になるとあまりにも多岐にわたる議論になって、とても収拾がつかなくなるでしょうし、鏡像問題の枠を超えてしまいます。ただし、鏡像問題で重要な要素である光学あるいは幾何光学的に定義される「像」については、明確にして理解しておく必要があります。というのも、そもそも鏡像が光の存在下で生じていることはまあ、光学の知識などを知らなくても普通の人なら理解しているとはいえますが、なぜ実際に鏡で見ているように見えるのかということは、光学の知識なしでは絶対に理解できないからです。本当は眼のしくみについても理解しなければならないはずですが、それは当面ブラックボックスに入れておくとしても、光の直進と反射の理屈を知る必要があります。
鏡映反転の謎はプラトンを悩ませたと言われています。プラトンのような超天才でも鏡映反転の謎が解けなかった理由の少なくとも一つは、プラトンの時代には幾何光学が成立していなかったためでしょう。プラトンは幾何学者ではあったけれども幾何光学はまだ存在もしていなかったというわけですね。しかしプラトンは当時のあり合わせの知識で安易な説明を付けて満足するようなことはしなかったわけで、これは逆にプラトンが真の科学者でもあったことを示すものだと思います。
ということで、鏡映反転の問題がまともに議論されるようになったのは光学の、少なくとも光の直進と反射の法則が明らかになった後、つまりヨーロッパのルネッサンス時代以降のことになるのではないでしょうか。 たとえば哲学者のカント。
数学者で科学者でもあったカントが鏡映反転の問題を考えたと言われています。これは私見ですが、カントはどうも鏡映反転の問題を考えているうちに、いつしかもっと抽象的な空間の問題に移行してしまい、具体的な鏡映反転の問題を置き去りにしてしまったように思います。というのは鏡映反転の問題からもっと抽象的な空間の問題に移行することで、後の学者などによって幾何学的な対掌体の概念がやがて明らかになってくるからです。ここではこういう歴史的な問題は余談ということにしておきます。(注:私はプロレゴ-メナの日本語訳しかカントの著作は知らないので、上記カントの考察について考えたことは、プロレゴ-メナから読み取れる限りのことです。)
さて、以上のような次第で幾何光学の基礎、少なくとも幾何光学における像の定義を知らずに鏡映反転のメカニズムを考察することは現代では無意味であることが分かります。
とは言え、幾何光学で「像」の概念が完璧に定義されているかといえば、必ずしもそうはいえず、「像」の本質を問うような議論はあまりされていないのではないでしょうか? ただし、幾何光学(この場合は結像光学という分野もあるようですが)で取り扱われる限りの実像と虚像の定義、少なくともそれらの像が成立する位置や大きさなどは厳密に定義されているはずで、それらを正しく扱わない限り、幾何光学を論じること自体が無意味です。
日本人の場合、少なくとも高校までに幾何光学の基礎、光の直進と反射の理論については習っているのではないでしょうか?例え習っただけで十分に理解していないとしても、 少なくとも専門家には鏡像成立のメカニズムが理解されていることを納得しているので、鏡を見ても不思議に思わず、安心していられるのではないでしょうか。光の反射による鏡映のメカニズムが知られるまでは、鏡の作用は日本でも神秘現象だったのです。もっとも何らかの自然現象であるらしいことは経験的に分かっていたでしょうし、多分、江戸時代くらいにもなれば、殆どの場合は特別な神秘現象ではないらしいという程度のことも経験的には感づいていたとは思いますが。とは言え、鏡や水面の向こう側にこちら側の景色が映って見えること自体は謎であり、不思議なことだったのです。幾何光学によって少なくとも大幅にこの謎が解明されたわけですから、幾何光学の理論を無視したり、理解せずに鏡映反転の謎を解くことは無謀であり、知的後退と言わざるをえません。
ただ、現在の科学は数多くの専門分野にわかれており、例えば小林秀雄もどこかで、「科学者も自分の専門分野以外のことでは素人と変わらない」と書いていたように記憶しています。 それは全くそのとおりでしょう。前回に考察したHaig氏の説明を見ても、Haig氏は心理学者を、「光学を知らない」ということで批判していますが、当のHaig氏は光という物理的な存在について考察しているだけで、「像」という物理的ではない存在については非常に無理解のままです。一方の高野先生は幾何光学の基本的な概念を理解していません。これについてはHaig氏の心理学者に対する批判がそのまま該当するのかも知れません。
そうはいっても、科学が多くの専門分野に分かれているとはいえ、心理学は感覚や知覚の問題を扱わざるを得ないのであって、生理学を通じて物理化学と不可分とも言えるのではないでしょうか。だからこそ、マッハのような物理学者が心理学の発展に貢献しているのではないのでしょうか? ですから、少なくとも知覚心理学のような分野で、特に視覚に関連する分野で幾何光学を正しく、少なくとも必要な範囲で、理解していないことは致命的な結果をもたらすと言わざるを得ません。
そこで前回の続きですが、ここでもう一度Haig論文の図を次に引用します。
前回は私の考えによるHaig説の批判でした。その際、特に必要はなかったのでHaig説の具体的で詳細な説明はしませんでしたが、今回、高野先生によるHaig説批判を検討するに当たってはそうも行かないので、まず簡単にHaig説の主張そのものを要約しておきます。なお、以下の数節は今回のテーマ「虚像について」とは必ずしも関係なく、また煩雑なので、青色文字にしてあります。適当に飛ばしてお読みください。
Haig説では次の2つの異なる方法(どちらも上図に基づいていますが)で鏡映の左右逆転を説明しています。ただし基本的な原因が光の反射の法則にあるとする点が両者に共通しています(Morris氏や高野先生などはこれを「光学仮説」と呼んでいます。要するに幾何光学に基づく説明のことです):
① 上図で顔(face、右側の四角形)から出る光を鏡(mirror、左側の四角形)で反射させてEの位置で見た像を、Fの位置(conjugate point、共役点)で直接見た像と比較すると、上下(AC)は逆にならないが、左右(BD)は逆になる
② 上図で(a)のように入射光の作る面(APQC)と反射光の作る面(PQE)が重ならない方向(Tangential)の場合は方向が逆転しないのに対して(b)のように、入射光の作る面(STBD)と反射光が作る面(STE)が重なる(同一面)場合には方向が逆転して見える
以上の①と②の二通りの説明をしているわけですが、高野先生はまずMorris(1993)を引用して①を否定しています。その根拠は、Eの位置で鏡像を見ている人がFの位置に歩いて移動して直接(鏡を透過させるか鏡を取り除いて)顔を見た場合を鏡像と比較すると確かに左右だけが逆転するが、歩いて移動せずに上から飛び込むように、つまり逆立ちした状態でFの位置まで移動した場合は左右ではなく上下が逆転するではないか?だからHaig説は間違いである、と言うものです。
端的に言ってこのMorris(1993)による批判は間違っています。確かに観察者が上から飛び込むように、つまり逆立ちした状態でEからFに移動したとすれば左右ではなく上下で逆転しますが、だからといって、普通に歩いてEからFに移動した場合に左右が逆転することまでを否定することにはなりません。何れの場合も上下か左右のどちらかで逆転しています。要するにMorris(1993)の説明はHaig説に条件を付けているだけであって、これでHaig説のすべてを全面的に否定することはできないのです。前回記事で私が説明したように、対象が平面であって「鏡映で左右が逆転するのはなぜか?」という問いかけに対する回答である限り、Haig説(上記①の説明)が間違いであるとは言えないのです。
次にTakano()では上記②の説明を、次のように否定しています。「 If his explanation were correct, an up-down reversal would be observed by the eye located on the elongation of AC in Figure I A because the optical layout becomes essentially identical to that in Figure I B, producing what Haig called a "sagittal view" (pp. 864865).」
これは正当な批判であると考えられます。確かにACの延長線上、例えばCの下方で鏡を見た場合は上下方向をHaig(1993)のいう「Sagittal」面で見ているのにも関わらず上下が逆転して見えることにはなりません。この点でHaig説は誤りです。ただし、この説明が誤りであるからといって①の説明までを否定できるわけではありません。①の説明と②の説明は、両者が光反射の法則に基づいている点で共通していますが、一方が否定されたら他方も否定されるという関係ではありません。①の説明が、例え条件付きであっても有効である以上、「光学仮説」を全面的に否定することはできないのです。
Haig説の問題は、「Sagittal」という用語の用い方にもあるようです。手元にあった2つの理化学事典(岩波理化学事典と研究社理化学和英辞典)で調べてみましたが、光学にはSagittal plane、Sagittal rayなどの専門用語があるものの、「回点対称な結像系」で定義される用語だそうです。つまり凸レンズなどによる実像についてのみ、意味を持つ用語ではないかと思います。鏡像は虚像であるし、文字通り鏡面対称であって回転対称な結像系ではなく、光学用語としての「Sagittal」にはあまり意味がないと考えるのですがどうでしょうか。
前回の記事で私は「Sagittal」を解剖学用語として理解したのですが、確かに光学、具体的には結像光学でこの用語が使われているようです。しかし鏡像の問題では結像光学で使われるこの用語と概念に意味はないことになります。ただし、この用語「Sagittal」を解剖学の用語と意味で解釈すると鏡像問題において重要な意味を与えることができます。(解剖学用語としてのSagittalについては、インターネットで画像検索すればすぐに分かります)。
というのは、解剖学用語としての「Sagittal」は人間の上下・前後・左右に関わる用語であるからです。上記Morris(1993)の批判に見られるように、観察者の姿勢と向きは鏡映反転において重要な意味を持っています。ところがHaig説では観察者を含めてすべて1つの点でしか表現されていないのです。そこにSagittalという解剖学にある用語が入ってきたので、私はその前後をきちんと読まずに、ここに観察者の姿勢と方向の要因が加えられているのかなと考えた次第なのです。しかし光学的な定義ではSagittalにさしたる意味はなさそうです。
もしかすると、Haig説では観察者、つまりEで示される眼を持つ観察者の上下・前後・左右の三つの軸の一つである前後軸が、光学でいうSagittal planeという概念にすり替えられているのではないかと思われるのです。上図には観察者は眼の位置だけで表現されています。しかし、観察者が正立して鏡面に向かっていることは暗黙の中に了解されています。Eの位置にいる観察者がFの位置に移動するとすれば、観察者の前後軸と左右軸は逆転しますが、上下軸は逆転しません。長くなるのでこの問題についてはこれまでとします。
以上はHaig説の問題点あるいは誤りと言えますが、今回のテーマである虚像に関連する問題として高野説には上記引用の後の2つの節で重要な誤りが見つかります。引用すると長くなるので省略しますが、次の節とその次の節では、鏡像を、鏡面上に生じた平面パターンのことであると認識した上で議論が展開されています。現に、Haig(1993)からの引用された上図に高野先生が追加された説明には、「The mirror image, PQ, of the vertical line segment,」と書かれていますが、PQをmirror imageというのは明らかな誤りで、幾何光学の定義に反しています。PQは、鏡像でも鏡像中の線分でもありません。前回の記事で私が述べたように、この図には鏡像は表現されていません。この部分を分析してみようと思いましたが、これらの節では「Optical layout」という定義されない曖昧な表現がキーワードのように使われているので、分析するのは非常に難しいです。ただ、この用語が幾何光学で定義されている虚像(この場合は鏡像)を意味しているように受取ることができます。とすれば、高野先生はここで鏡像の二重定義を行っていることになります。これは高野説のその後の展開の基礎になっていますので、この辺の論理を明確にしておくことは重要だと思います。高野先生は鏡像が平面であるという理由で鏡像が相手の対掌体であることを否定しておられますが、幾何光学で定義される鏡像は平面パターンではなく、鏡の表面に生じるものでもないのです。
まず、この文脈で言えばOptical layoutという表現で何を意味しているのかを具体的に、明確にする必要があります。Layoutの本来の意味からは外れますが、上図のような幾何光学の光路図を指しているのでしょうか?その場合は場合によっては具体的にどの図のどの部分であるかを示す必要もあります。あるいは新たに図を作成する必要があるかも知れません。
ここでは、私は専門家でもないので詳しく説明しませんが、幾何光学では鏡像を含めて虚像について厳密にその位置と大きさ、また方向もきちんと定義されています。それらの定義に反する説明は現在の幾何光学の大系そのものを否定することになり、否定するのであればその根拠を示す必要があります。
とはいえ、幾何光学で厳密に定義される虚像というのは、最初の方でも述べましたが、位置とか大きさとか、要するに技術的な展開が可能な範囲でしか定義されず、像そのものについて何ら明確な定義はおこなわれていないように思います。そもそも簡単に辞書的な「定義」で済ませることは不可能な問題であるのかも知れません。しかしそれこそが心理学者、認知科学者、あるいは認識論学者の仕事であり、使命なのではないでしょうか?
虚像について考えることは像そのものについて考える上で最上の手がかりです。
今回の引用参考文献:
Nigel D Haig, 1993 "Reflections on inversion and reversion" Perception1993, volume 22, pages 863-868
Reg C Morris, 1993 "Mirror image reversal: Is what we see what we
present?" Perception, 1993, volume 22, pages 869-876
Yohtaro Takano, 1998 "Why does a mirror image look left-right reversed?
A hypothesis of multiple processes" Psychonomic Bulletin & Review 1998,5 (1), 37-55
以上(2017年3月15日 田中潤一)
登録:
コメント (Atom)